ImageNet用ResNet50での信号の流れを追ってみた

　最近、専門書をワクワクしながら読み進めるというような経験はあまり無くなってしまったが、唯一の例外がオライリー・ジャパンから出ている「ゼロから作るDeep Learning①〜③」のシリーズです。③はDeep Learningの「フレームワーク」の作り方についてですが、PFI/PFNのChainerのフレームワークにかなり近いものになっているようです。②は「自然言語処理」に関する内容だったので、自分としては、後、「音声処理」と「強化学習」の２冊を是非上梓して頂きたいなと思っています。

　カレントなプログラミングにおいては、フレームワークは重要な技術の一つになっています。有名なものとしては、Webアプリケーションのフレームワーク（MVCモデル）があります。Rubyが世界的に使われるようになったきっかけは、Ruby on Railsがあったからです。またPHPにもCakePHP、Symfony、Laravel、etc、色々なフレームワークがありますし、PythonにはDjangoがあります。私は、機械学習用のオープンソースのフレームワークとしては、Tensorflow(+Keras)とChainerの２つを使っていますが、その他にもCaffe、PyTorch、etc、もあります。

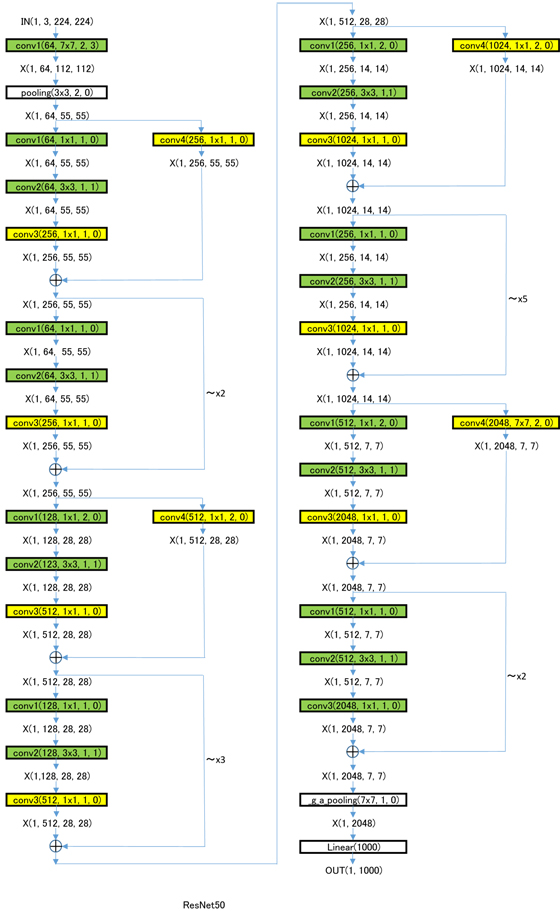
　③の第５ステージのステップ58では、実際にDeZeroのフレームワークを使ってImageNet用にVGG16のCNNを構築する例が出ていますが、そのおまけで、ResNetのコードも掲載されていたので、そこからResNetでの信号の流れを追ってみました。（ResNetはResNet50、ResNet101、ResNet152の３種類ありますが、その中で一番簡単なResNet50のものを掲載してあります。）ResNetもVGG16と同様に既に調整済みのパラメータで公開されているものをダウンロードする事で、実物の環境をDeZero上で再現出来るようになっています。

　ResNetの構成はVGG16に比べてかなり複雑なので、下記の参考文献のTable 1.あたりを参考にしながら下図を見ていただければ、やっていることがよく分かると思います。

下図において、

　・X(Number, Channel, Height, Width)　= 入出力信号のサイズ

　・conv1~4(Channel, kernel_size, stride, pad) = 下の「緑のブロック」、または「黄色のブロック」（()内は   Conv2dの引数）

　・緑のブロック = Conv2d(Channel, kernel_size, stride, pad) -> BatchNorm() -> relu()の３層構造

　・黄色のブロック = Conv2d(Channel, kernel_size, stride, pad) -> BatchNorm()の２層構造 

　・加算演算子記号 = 加算器 -> relu()の２層構造

　・~xN = ~のブロックをN回繰り返す

です。

（参考文献） https://arxiv.org/pdf/1512.03385.pdf

by チイ

モンティ・ホール問題

　最近、一般向けに書かれた人口知能の解説書の中に、「モンティ・ホール問題」という名前をよく見かけるようになりました。モンティ・ホール問題は、別名「三つの扉問題」や「三囚人問題」と同種の問題です。一見すると直観に反するような問題なのですが、最近は日本の国会でも統計で嘘をつく様な問題が取り沙汰されているので、頭の体操だと思って考えてみると面白いです。三つの扉問題とは以下のような問題です。

（問題１）

三つの扉A、B、Cがあり、司会者とゲストがいる。司会者はゲストの見ていない所で、一つの扉の後ろに賞品を隠す。ゲストに扉を選ばせ、賞品の隠されている扉（当たり）を言い当てたらゲストはその賞品を獲得できるものとする。ゲストは扉Aを選んだとする。選んだ扉を開ける前に司会者は、「私は当たりの扉を知っていますので、残った二つの扉B、Cのうち外れの扉を開けてお見せしましょう」といって実際に外れの扉を開け、確かに外れであることを確認させる。その扉がBであったとする。そして、さらに司会者はゲストに、「最初に選んだ扉Aのままでも良いですが、まだ開けていない扉Cに変えても構いません」と言う。この時、以下の問いに答えよ。

（１）ゲストが扉Aを選んだ時点で、その扉が当たりである確率を求めよ。

（２）司会者が扉Bを開けて、それが外れであることを示した時点で扉Aが当たりである確率を求めよ。

（３）ゲストのとるべき行動について、以下のいずれが正しいか？

１）　選択を変えてはならない

２）　選択をAからCに変えるべきである

３）　選択を変えても変えなくても同じである

答えは先に言ってしまうと、

（１） 1/3

（２） 1/3

（３） ２）

となります。

（問題１の解説）

S（原因）は、扉A、B、Cが当たりであることをS=ωA、S=ωB、S=ωCとすると、事前確率は

P(ωA) =  P(ωB) = P(ωC) = 1/3 

になります。

X（結果）は、司会者が扉Bを開けることをX=oB、扉Cを開けることをX=oCで表すことにすると、

求めたいのは、司会者が扉Bを開けたという条件の下で、扉Aが当たりである事後確率は、P(ωA | oB)であるので、

次のように場合分けをして、

（１）扉Aが当たりの場合、P(oB | ωA) = 1/2（P(oC | ωA) = 1/2）

（２）扉Bが当たりの場合　P(oB | ωB) = 0（P(oC | ωB) = 1）

（３）扉Cが当たりの場合　P(oB | ωC) = 1（P(oC | ωC) = 0）

となります。

これを条件付き確率の問題として考えると、下図１のような図が描けて、司会者が扉Bを開けて見せるのは水色部(a)、(b)となり、その内扉Aが当たりであるのは(a)の部分であるので、

P(ωA | oB)  = (a) / {(a) + (b)} = 1/3

となります。

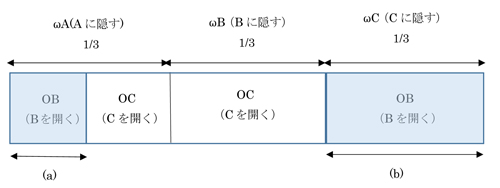
　　　　　　　　　　図１　司会者が正解を知っている場合

このことは、ベイズの定理を使うと、代数的にももっと明白に理解することができますが、やっていることは上の条件付き確率と同じことになります。

P(ωA | oB)

 = P(ωA )P(oB | ωA) / {P(ωA )P(oB | ωA) + P(ωB)P(oB | ωB)+ P(ωC )P(oB | ωC)}

 = (1/3)x(1/2) / {(1/3)x(1/2) + (1/3)x0 + (1/3)x1}

 = 1/3

同様に、

P(ωB | oB) = 0

P(ωC| oB) = 2/3

となります。

（問題２）

もう一つの問題は、（問題１）の設定で、ゲストも司会者も正解を知らない場合です。すなわち、司会者、ゲスト以外の第三者が賞品を隠し、ゲストが扉Aを選んだ後、正解を知らない司会者が扉Bを開けたら外れだったという場合である。

この場合、答えは、

（１） 1/3

（２） 1/2

（３） ３）

となります。

（問題２の解説）

X（結果）は、司会者が扉Bを開けて外れであることをX=oB、当たりであることをX=oB*、扉Cを開けて外れであることをX=oC、当たりであることをX=oC*で表すと、

求めたいのは、司会者が扉Bを開て外れであることが分かったという条件の下で、扉Aが当たりである事後確率は、P(ωA | oB)であるので、

次のように場合分けをして、

（１）扉Aが当たりの場合、P(oB | ωA) = 1/2（P(oC | ωA) = 1/2、P(oB* | ωA) = P(oC* | ωA) = 0）

（２）扉Bが当たりの場合　P(oB | ωB) = 0（P(oB* | ωB) = P(oC | ωB) = 1/2、P(oC* | ωB) = 0）

（３）扉Cが当たりの場合　P(oB | ωC) = 1/2（P(oC*| ωC) = 1/2、P(oB* | ωC) = P(oC | ωC) = 0）

これを条件付き確率の問題として考えると、下図２のような図が描けて、司会者が扉Bを開けて外れであるのは水色部(c)、(d)となり、その内扉Aが当たりであるのは(c)の部分であるので、

P(ωA | oB)  = (c) / {(c) + (d)} = 1/2

となります。

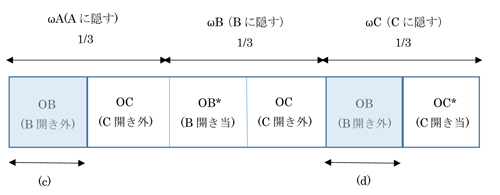
　　　　　　　　　　　図２　司会者が正解を知らない場合

これはまた、ベイズの定理から、

P(ωA | oB)

 = (1/3)x(1/2) / {(1/3)x(1/2) + (1/3)x0 + (1/3)x(1/2)}

 = 1/2

となります。

同様に、

P(ωB | oB) = 0

P(ωC| oB) = 1/2

となります。

　また、これらの発展形として、扉の数を３からn（＞３）に増やした同様のケースも考えてみるといいかもしれません。理系の難関大を受験される方は、モンティ・ホール問題は常識として知っておいた方がいいと思います。実際にそれは条件付き確率の問題として解くことができますが、ベイズの定理を知っていれば、その理解がより深いものになると思います。ベイズの定理自体は、条件付き確率から簡単に導き出せるものなので、罹患率の簡単なベイズ更新の計算くらいはやっておいた方がいいかもしれません。

　後、どうしても納得できなという人は、実際に自分でプログラムを書いて実験してみるという方法もあります。ただ、そんな時間は無いよという人のために、下記に実際にそのプログラムを公開してくれている人のURLを貼っておきました。数分くらいで、ソースコードをコピペして動かすことができます。

https://qiita.com/mastar_3104/items/a227f3665b95ffe73a36

by  チイ

Batch Normalization（バッチ正規化）

　たまたまYouTubeを見ていたら、2019年センター数学の数学IA第2問の統計分野の問題が良問だということで、YouTubeにその問題の解説をアップしている人の動画がありました。見ていたら、なんとDeep Learningなどでもよく使われる機械学習のテクニックである「Batch Normalization」の基礎的な計算問題でした。

　実は、バッチ正規化は「ゼロから作るDeep Learning（オライリー・ジャパン）」の第6章「学習に関するテクニック」の中の6.3節Batch Normalizationで解説されています。今年度の出題者が統計分野の問題として、バッチ正規化の中から関係ありそうなものを選んで出題したのかどうかは分かりませんが、高校の数学も今の時代にマッチした分野はどんどん積極的に取り入れていけばいいと思います。

　バッチ正規化とは、2015年にGoogleから提案された比較的新しい手法で、学習を行う際のミニバッチを単位として、ミニバッチごとに下記式により正規化を行います。アイデアとしては、各層で適度な広がりを持つように、”強制的”にアクティベーションの分布を調整しようというものです。（イメージ的には塔を構成しているブロックが横に大きく動くと不安定なものになるのを、ブロックを真っ直ぐ上に積み上げるようなイメージ。）結果、深層学習のトレイニングの学習スピードを加速させるなどのメリットがあります。

　μ_{B  ←}  (1/m)Σ_i=1~mx_i

    σ_B²  ←  (1/m)Σ_i=1~m(x_i - μ_B)²

    x̄_i  ←  (x_i - μ_B) / (√(σ_B² + ε))

    y_i  ←  γ x̄_i + β

　やっていことは、ミニバッチの入力データ{x₁,x₂,・・・,x_m}を、平均０、分散１のデータ{x̄₁,x̄₂,・・・,x̄_m}に変換するというシンプルなものです。試験の中では、この変換後のデータの平均（０）と分散（１）の値を問うという設問になっています。上記書籍の中では、ここはもう当たり前にそうなるものだとして特に証明などはされていませんが、まだ確認されてない方はこの機会に一度計算してみるといいと思います。

　さらにバッチ正規化レイヤは、この正規化されたデータに対して、固有のスケールとシフトで変換を行います。（一番最後の式）ここで、γとβはパラメータで、初期値γ=1、β=0からスタートして、学習によって適した値に調整されていきます。学習の仕方はこの書籍で紹介されている下記の文献（１）、（２）の中の計算グラフに従って、common/layers.pyのBatchNormalizationクラスに記述されているので、インプリメンテーションに自信のない方は、一度その中に書かれてあるPythonコードを読めば何をやっているかがよく分かると思います。

　機械学習を勉強されている方で、バッチ正規化って何だったかもう忘れてしまったという方は、今年度のセンター数学の統計の問題としても出題されたので、この機会に理解を完全なものにしてみてはどうでしょうか？

(1) https://arxiv.org/pdf/1502.03167.pdf

(2) https://kratzert.github.io/2016/02/12/understanding-the-gradient-flow-through-the-batch-normalization-layer.html

３変数鶴亀算〜南雲忠一効果〜

　「翼君は、60円、90円、120円の３種類の切手を合わせて17枚買って1440円となりました。60円の切手は90円の切手の2倍の枚数を買いました。それぞれの切手の枚数は何枚になるでしょうか？」

　これは中学受験の「３変数の鶴亀算」の問題です。大人なら３変数の方程式を立てて誰でも解くことができますが、貴方はこれを算数の問題として鶴亀算を使って解くことが出来ますか？通常、学校で教わる鶴亀算は２変数を扱います。この問題の難しさはそれが３変数あると言う事です。最近ちょっとしたきっかけで算数の鶴亀算の問題をみていた時に、３変数の鶴亀算ってあるのかな？とふと思って探してみるとありました。３変数の鶴亀算は難関中高一貫校の算数の問題としてよく出されるみたいです。

　鶴亀算は「面積図」と言うのを描いてみるとよく分かります。（私が小６の頃にはこの考え方は教わらなかった様に思うが？？）２変数の場合は、面積図を描くと「こぶ」がひとつだけできて、そのこぶの面積が求まれば鶴亀算は解けたことになるのですが、３変数の場合はこぶが２つできてしまって、さてどうするの？って言う話です。

　ヒントは２つのこぶをひとつに均します。上の例で言うと、「90円1枚と60円2枚の１セットを考え、１セット210円の中に平均値段が70円の切手が3枚ある」と言う風に考えます。そすると70円切手と120円切手が合わせて17枚ある通常の２変数の鶴亀算になります。後は、興味のある方は続きを最後まで鶴亀算で解いてみてください。

　何故、こんな事を書いたかと言うと、普通は３変数、４変数のものを鶴亀算を使って解こうとする人なんていないと言う事です。それは代数方程式を使って解いた方がずっと楽だからです。鶴亀算には代数方程式ほどの一般性や拡張性が乏しいと言う事です。でも受験では皆が鶴亀算の応用問題の対策をしており、ありきたりの２変数では全員が解けてしまうので、わざとに小難しい３変数の問題を作っているわけです。

　中学受験のを経験した様な人でも、中学になって代数方程式を習った途端に、鶴亀算は頭の中から完全に消えてなくなってしまうと思います。（受験であんなに苦労させられた鶴亀算なのに!!）逆に中学になってからも代数方程式の問題を鶴亀算で解いたりしていると、周りから「お前バカなんじゃない!!」と言って笑われてしまいます。でも問題によっては何でもかんでもx、y、zと置いて代数方程式を使って解くより、鶴亀算を使って解いた方が簡単でずっと速い様な場合もあります。本来は、大人になっても問題によって、両者を使い分けられる様な教え方をすべきなのです。

　日本海軍は昭和に入ってからいわゆる「ペーパーエリート」になってから没落しました。山本五十六も南雲忠一も当時のペーパーエリートです。「超ウルトラ戦艦クイズ」を解いてきた人達なのです。でもその能力は「空母」の時代には全く役に立ちませんでした。まだ答えのない問題を解く必要があったからです。私はこれを「南雲忠一効果」と呼んでいます。日本の受験制度は度が過ぎるといつも南雲忠一効果に陥って時代から取り残されていきます。

by チイ

　

RBMのBGSやCDやPCDってどれくらい違うのだろうか？

　RBM(制約付きボルツマンマシン)のプレトレーニング（教師なし学習）の手法である、BGS(ブロック化ギブスサンプリング)やCD(コントラスティブ・ダイバージェンス法)やPCD(持続的コントラスティブ・ダイバージェンス法）について、実際の学習データを用いて、その学習の習得過程をトレースしてみた。

　一般に、RBMの<vi>modelや<hi>modelや<vihj>model（注１）などは組み合わせ爆発を起こして計算することができないので、BGSを用いて計算されるが、ギブスサンプリングはバーンインに要する時間を長く取らないといけなかったりするので、計算時間が膨大になってしまう。そこで開発された時間短縮の手法が、CDやPCDと言った簡易的な手法になる。今回の実験では、BGSとCDではCD-1とCD-5の２種類とPCD（CD-1のv1の結果を次のパラメータ更新の頭で使う様にチェインで繋いでいったもの）の４種類を行っている。

　データは、４ビットのバイナリーデータ（従って、16種類のデータになる）をランダムに1000個発生させて、エポック毎に10個のデータを使ってミニバッチ学習を100回行っている。入力層が4個で隠れ層が3個のRBMを構成して、パラメータは、w=(3, 4)、b=(,4)、c=(,3)としてミニバッチ学習毎に更新を行っている。パラメータ更新は、BGSはMLP深層学習（岡谷貴之著）p143の式（8.18a)〜(8.18c）を（注２）、CDはp145の式（8.19a)〜(8.19c)のアルゴリズムを用いて行っている。

　図1.1〜1.3ではW（重み）の初期化を、それぞれの手法ごとでランダムな正規分布で行っている（従って４種類の手法でWの初期値は違っている）のに対して、図2.1〜2.3では全ての手法でランダムな一様分布（従って４種類の手法でWの初期値は同じ）を用いて行っている。パラメータの初期値を揃えた場合は、対数尤度、KL距離共に学習過程のバラツキは比較的小さなものになるが、違った場合のバラツキは大きくなっているのが分かる。（注３）

　図1.1と図2.1は、 （式１）でエポック毎のKL（カルバック・ライブラー）距離を計算している。

　　　DKL(P||Q) = Σi P(i)log(P(i) / Q(i))   （式１）

　ここで、P(i)はデータの確率分布、Q(i)はモデルの確率分布で、Q(i)は（式２）から計算している。KL距離は、学習が進むに連れて最小値になって行っているのが分かる。

　　　p(v | θ) = exp(Σi∈V bivi) Πj∈H (1 + exp(λj)) / Z(θ)    （式２）

　　　(ここで、λj = cj + Σ i∈V wijvi)

　図1.2と図2.2は、（式３）でエポック毎の対数尤度を計算している。

　　　LD(θ) = logΠμ=1~N p(v^(μ)  | θ)

                  = Σμ=1~N (Σi∈V bivi^(μ) + Σj∈H log(1 + exp(λj^(μ))) - logZ(θ))   （式３）

　対数尤度は、DKLとは逆に、学習が進むに連れて、最大値になって行っているのが分かる。４つの手法が大体同じくらいの最大値で平衡した時点で学習を終了させている。

　図1.3と図2.3は学習が終了した時点でのそれぞれの手法でのモデルの確率分布を示している。４つの手法ともに、実際のデータの確率分布の特徴を良く再現できている事が分かる。プレトレーニングなのでこれくらいの精度でデータの特徴を抽出できれば十分の様な気がする。

（注１）<.>は期待値を表す。

（注２）バーンインは通常は1000回以上取るのが理想だが、時間がかかり過ぎるので（これはミニバッチの度に行う必要がある）、100回で行って見たものとあまり差がなかったので100回で回している。その後ミニバッチと同じ10点をサンプリングして平均値を求めている。

（注３）一般的に、特にW（重み）の初期値によりそれぞれの手法での収束過程は上下関係なども含めて大きく変わってしまう様である。また収束にもっと時間を要してしまう様な場合もある。目安としては、対数尤度又はKL距離が最終的に全ての手法で大体同じくらいの値で収束する様な初期値を取るのがベストであると考えられるが、何れにしてもプレトレーニングなので、ある程度の回数を回して収束すればそれで良しとしても特に問題はない様に思う。

by  チイ

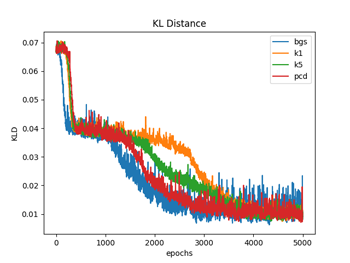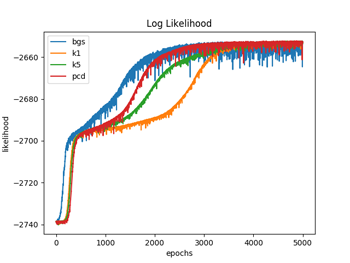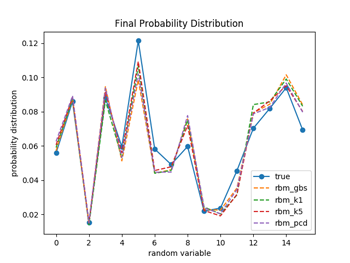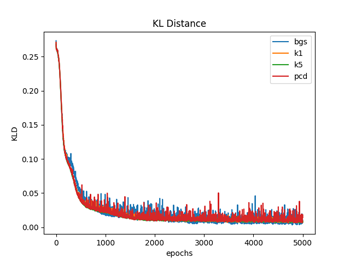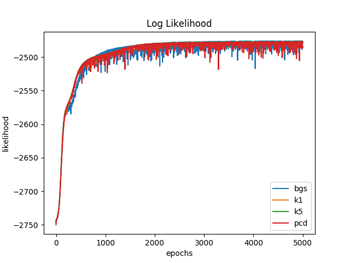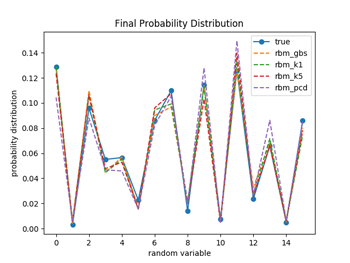図1.1図1.2図1.3図2.1図2.2図2.3

コンピュータ・サイエンスにみる学びの多様性

　最近、文春新書から「知立国家 イスラエル」（米山伸郎著）という題名の新書が出版されて、大変興味深く読ませていただいたが、その中で特に気になった箇所があった。今の日本のコンピュータ・サイエンスの現状をそのまま表している数字のように思えた。「コンピュータ・サイエンスで有名な世界の大学のトップ30の中に、イスラエルの大学が4校も入っているのに対して、日本の大学は一つも入っていない。」

　これは最近の世界の大学ランキングで日本の最高学府である東大が40番台の前半であるのを考えると、そんなに驚く様な数字ではないのかもしれないが、21世紀のこれからの将来展望を考えた時、日本産業にとっては切実な問題になってくるように思われる。ちなみにイスラエルでは16歳から選抜される軍関係のトップ頭脳集団「タルピオット」では、３年間かけて高等数学、物理学、コンピュータ・サイエンスの３学科を徹底的に叩き込まれるようだ。（日本の大学で４年かけて１科目を専攻するのを３年間で３科目やってしまう。）中でも、コンピュータ・サイエンスは国策として最も力を入れている分野でもあるらしい。

　そもそも日本にはコンピュータ・サイエンス学科や学部というものは基本的には存在しない。東大や京大にもない。あるのは工学部の中に、「情報ナンチャラ学科」みたいなものしかない。前にも書いたが、多くの日本人はコンピュータはサイエンスだとは思っていないので（注）、まず「コンピュータ・サイエンス」という言葉自体にかなりの抵抗がある。そしてやっている事はといえば、そのほとんどがハードウエアに関係する事が中心だ。思うに21世紀のコンピュータ・サイエンスでは７〜８割くらいがソフトウエアに関係するものになると思う。cognitive computing用の新しいハードウエアももちろん必要になってくるが、それもソフトウエアがあってのハードウエアだと思う。

　今のままの状態だったら、これからのAI時代、本物のコンピュータ・サイエンスを学びたい人は海外のWASP系の大学やイスラエルの大学に留学した方がいいのかもしれない。学びの多様性という意味では、ビルゲイツもマーク・ザッカーバーグもIT関連で成功している人の多くは、高校時代に学校にも行かないでプログラミングに熱中し、大学では起業して中退している。逆にラリーペイジやセルゲイブリンのようにコンピュータ・サイエンスの名門校で大学院まで進学して勉強したような人達もいる。ハーバードの数学科に入るような人も小中学校で飛び級した人とか数学オリンピックでメダルを取った人達とかで、少なくともSAT（日本の大学受験に相当するもの）の点数で選んでいるような人はほとんどいないと思う。

　現在の日本の大学受験にはコンピュータ・サイエンスはない。数学はというと、線型代数は２行２列の行列止まりで行列式のレベルにも行っていない。ベクトルは内積止まりでベクトル解析はまだ先の先。微積分は変数分離止まりで線形微分方程式にさえも行っていない。確率は条件付き確率止まりで、現在のベイズ全盛期に全く対応できていない。物理はといえば、力学は微積を使わないで力関係の図を描いて代数に当てはめるような、もう中学でやったらいいようなレベルのことを今だにやっているし（17世紀にニュートンが微積を使って力学を完成させたレベルにすら行っていない）、電磁気は、マクスウェルの方程式も知らないで、受動素子だけの交流の回路の問題や、直流のコンデンサの開け閉めのようなくだらない問題をやっている。

　20世紀はそれでも工学部で猫も杓子も電子回路さえ作っていればよかった時代には、皆が一律に全く同じ学びをしていればよかったのかもしれない。しかし、21世紀の時代には全くそぐわない内容になってしまっていると思うのは私だけだろうか？イスラエルの国家戦略（目的）はただ一つで、それは「生存」するということ。前にも書いたがユダヤ人は全ての点において日本人とは真逆の特性を持っている。その彼らが「生存」を第一の戦略としてあげているという事は、逆に言えば、世界で一番すぐに滅びてしまう可能性があるのが日本ということになってしまう。上記日本の大学受験の内容が陳腐化してしまった時、学びの多様性のない日本はあっというまに陳腐化してしまうかもしれない。

（注）欧米のコンピュータ・サイエンスの理想形は、おそらく、サイエンス、工学（エンジニアリング）、数学の３つが三位一体となったような形をしていると思う。

by チイ

DPMによるクラスタリングの実験

　書籍「続・わかりやすいパターン認識」の第12章のディリクレ過程混合モデル（DPM）によるクラスタリング（ノンパラメトリックベイズ）の実験を、実際にpythonで実装して確認してみました。書籍では２種類のクラスタリング法の実験を行っていますが、今回はパラメータ推定も伴うクラスタリング法１の難しそうな方を行ってみました。前回の凸クラスタリング法もクラスタ数を推定する手法でしたが、ノンパラメトリックベイズはそのクラスタ数の推定を数学的にもっと美しくできるようにしたものです。ノンパラメトリックベイズとは、パラメータが無いということではなくて、「無限個のモデルを想定した無限個のパラメータを持ち得るベイズモデルの総称」のことです。

　初期状態は全ての500個の点がクラスタ０に所属する状態（c = 1）から始めています。その他ハイパーパラメータの値（式（12.33）と式（12.34））などは全て書籍のものに合わせて行っています。アルゴリズムはｐ260～261のStep１～Step５の「クラスタリング法１のアルゴリズム」に従ってpythonで実装してあります。

　ノンパラメトリックベイズではこれまでのクラスタリング法と違って、「サンプリング」という手法が用いられています。一つ目がｐ259の式（12.14）（下段の積分は、ｐ269の式（12.35）で行います）で、sk=ωi（i=1～c）とsk=ωnewの事後確率からskを「確率的に」決定します。私はここは、pythonのnumpy.random.uniform()を使って行っています。二番目が、ｐ259の式（12.15）（実際の計算は、ｐ269の式（12.37）を用いて計算する）で、事後分布からｃ個のクラスタのパラメータθi（i=1～ｃ）を「確率的に」決定します。具体的には、ｐ269の式（12.37）の正規ーウィッシャート分布からサンプリングしたθi=（μi, Λi-1）を求めることになります。まず、ウィッシャート分布のΛiをW(Λi; νc, Sq）（ここで、νcは式（12.42）から、Sqは式（12.38）で計算する）からサンプリングします。私はここは、pythonのscipy.stats.wishart()を使って行いました。このサンプリングしたΛiで式（12.41）からΛcを計算して、N(μi; μc, Λc-1)（ここで、μcは式（12.40）で計算する）からμiをサンプリングします。私はここは、pythonのscipy.stats.multivariate_normal()を使って行いました。

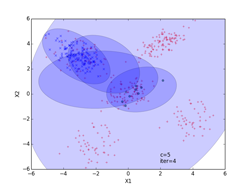
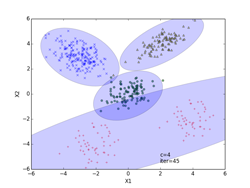
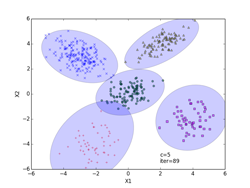
　ｐ261の式（12.16）のv（事後確率）の対数を取ったlogvの繰り返し数に対する変化を下図の「事後確率の変化」に示してあります。図中、logvが最大値となる繰り返し数の位置を赤の波線で示してあります。この時、s = {51, 199, 100, 100, 50}になりました（最下段のiter=89の図に相当）。またその右の「クラスタ数の変化」が、クラスタ数の繰り返し回数に対する変化を示した図になります。求めるｃ（クラスタ数）は図中で赤の波線で示した位置になり、その時c = 5の結果になりました。

　クラスタリングの結果を、iter=4,45,89について示してあります。クラスタリングされた点は、クラスタごとに違った形の違った色で示してあります。分布の輪郭線は、ｐ261のStep３から確率的に決定したθi=（μi, Λi-1）を使って描いています。最後のiter=89は、logｖのグラフでlogvが最大値となる繰り返し数で、図中で赤の波線で示してあります。その時のc（クラスタ数）=5になります。（クラスタ数のグラフの赤の波線のクラスタ数）

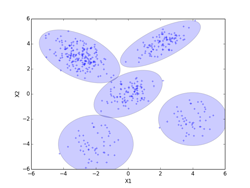
　　　　推定する共分散行列の分布

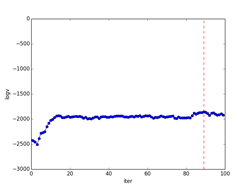
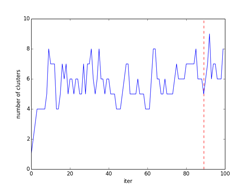
　　　　　　事後確率の変化　　　　　　　　　　　　クラスタ数の変化

　　           iter = 4（途中段階）　　　　　　　　 iter = 45（途中段階）

　　　     iter = 89（logvが最大）

by チイ

普遍文法

　日経サイエンスの５月号の特集「言語学の新潮流」で、「チョムスキーを超えて〜普遍文法は存在しない」という記事が掲載されていた。普遍文法は、「人は生得的に言語習得機構、すなわち言語機能（普遍文法）を持っている」という彼の仮説で、過去半世紀近くにわたって理論言語学を支配してきた。コンピュータの発達に伴って、計算論的アプローチを好む学者たちに支持されてきた。

　普遍文法自体も、時代の要請に合わせて、当初のものから→「原理とパラメータのアプローチ」→「計算的回帰性（再帰性）」へと変遷を遂げているが、文法的雛型に単語を当てはめる能力を子供達が生得的に持っているという基本的な考え方は変わらない。普遍文法は、下記の「語用論」も導入しているが、そこでの位置付けはあくまでも文法の脇役にとどまっていた。

　近年、普遍文法に代わる新しい仮説として「用法基盤モデル」と呼ばれるものが登場している。簡単にいうと、「子供は一般的な認知能力や他者の意図を理解する能力を用いて耳にした言葉から文法カテゴリーと規則を作り上げているという見方」。子供達が社会的相互作用の中で、認知処理機構（スキーマ化、習慣化、脱文脈化、自動化、etc）や制限機構（伝達意図推論）によって構文を使う経験を積むことで言語を習得しているとする。上に書いた主従関係が逆転したものとなっている。

 　言語の習得が人の新しい脳である大脳新皮質の発達と共に起こったことを考えると、言語はチョムスキーの言うようなハードウエア的なものよりももっとソフトウエア的なものだと思う。チョムスキーは偉大な学者だが、普遍文法仮説はおそらく間違っているように思う。ただ普遍文法は翻訳などの場合、コンピュータでは扱いやすいし、文の意味は理解していなくても、その文法規則にとりあえず当てはめさえすれば訳せてしまうが、一般的には変な訳になってしまう。逆に用法基盤モデルでコンピュータが言語を獲得できるようになった場合、人の子供と同じように、まずはコンピュータがその文の意味を理解できるように学習させることが不可欠になってくると思われる。

　今、全てのコンピュータ言語の中で、一番再帰的な言語といえばLISPになると思うが（LISPでは基本的には繰り返し文は存在せず、再帰で行う。）、言語処理用にLISPをもっと拡張したような言語は作れないものだろうか？（←適当に勝手なことを言っています^^;）いずれにしても、言語はチョムスキーも指摘しているように再帰性が鍵をにぎっているように思う。数年前に大川出版賞を受賞した、田中久美子氏著の「記号と再帰」という本の結語も、「人間の記号系は、再帰的な記号を自然に扱う。・・・今なお、コンピュータは再帰が苦手である。結局、コンピュータの発展は、再帰をどのように機械において扱うかという問題でありつづけるだろう。」というものだった。コンピュータが人間並みに「再帰」を扱えるようになった時、コンピュータは言語を習得していることだろう。

by  チイ

凸クラスタリング法の実験

　書籍、「続：わかりやすいパターン認識」の第10章ｐ208にある凸クラスタリング法による実験を、実際にpythonで実装して確かめてみました。凸クラスタリングのアルゴリズムは、ｐ206のもの（式（10.36）〜（10.45））を用いています。データは、前のEMアルゴリズムに使ったものと同じものを使っています。iter = 0の初期値は、書籍のものに合わせています。凸クラスタリングには、以下の様な特徴があります。

・ クラスタ数c を未知のまま推定する（メリット）

・ 凸計画問題なので、初期条件に依存せず、大域的最適解（最大点）となる（メリット）

・ 共分散行列σ^２が全てのクラスタで等しく、かつ等方的であるという前提（デメリット）

・パラメータσ^２は、恣意的に決める必要があり、直感に頼るしかない（デメリット）

　凸クラスタリングの実験を、以下の２通りの方法で試してみた。式（10.32）のσ²はσ² =1とした。なお、p208の図10.6の途中段階のグラフは今回は煩雑になるので掲載していません。一番最後のもの（final）だけを表示してあります。

・ノーマルケース

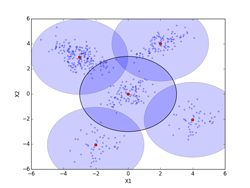
　全ての500個の点の事前確率π_iを最後まで愚直に計算した場合。iter=4000となった時点での、π_i > 0.01 の条件で選別して、6個のセントロイドが抽出された。(0, 0)のクラスタが２個のセントロイドとなったので、そのセントロイドの相加平均を求めている。（相加平均を求めたクラスタのσ² =1の等方的正規分布は輪郭線を太い黒で示してある。）図final_normalに示すように最終的なクラスタ数はc=５個になり、その最終的な事前確率は式（10.37）で再正規化を行ってπ_i= [0.396, 0.200, 0.205（注１）, 0.100, 0.099] となった。真の値、[0.4, 0.2, 0.2, 0.1, 0.1] に近い値になっている。一方セントロイドPは、P[5][2] = [[-3.014, 2.960], [1.994, 4.030], [0.006, -0.013], [3.991, -2.054], [-2.009, -4.059]]となった。（図でセントロイド位置は赤点で示してある。）

・カットケース

　予め定められた閾値（0.001/samples）以下となったπ_iは強制的に0に設定し、収束効率の改善を図ったもの。（ここで、samplesは、π_i ≠ 0のπ_iの個数で500から徐々に減っていくが、削除される度に式（10.37）で正規化を行っている。これに合わせて、π_i = 0のf_ik（p206のStep2の式）に対応する行も削除されていく。）最終的にiter=4000で、12個のセントロイドが抽出された。samples=12, f_ik  = (12, 500)となった。(-3, 3)クラスタのセントロイドが４個、(0, 0)クラスタのセントロイドが４個、(-2, -4)クラスタのセントロイドが２個となったので、それぞれのクラスタのセントロイドの相加平均を求めた。（相加平均を求めたクラスタのσ² =1の等方的正規分布は輪郭線を太い黒で示してある。）図final_cutに示すように最終的なクラスタ数はc=５個になり、その最終的な事前確率はπ_i = [0.395（注２）,  0.199,  0.206（注２）, 0.100, 0.100（注２）]となった。セントロイドPは、P[5][2] = [[-3.014, 2.960], [1.994, 4.030], [0.007, -0.011], [3.991, -2.054], [-2.008, -4.058]]となった。（図でセントロイド位置は赤点で示してある。）

（注１）(0, 0)のクラスタの２個の事前確率を足し算している。（0.1707 + 0.0340）

（注２）(-3, 3)、(0, 0)、(-2, 4)のクラスタの４個、４個、２個の事前確率をそれぞれ足し算している。

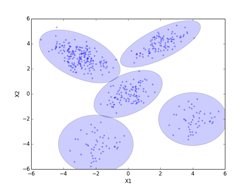
              推定する共分散行列の分布

  

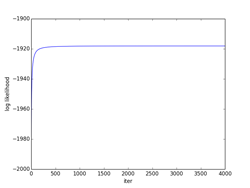
　　　　　　    final_normal                                   対数尤度（normal）

   

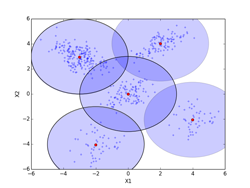
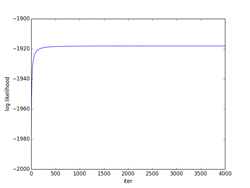
                         final_cut                                       対数尤度（cut）　

by チイ

K-means法によるクラスタリングの実験

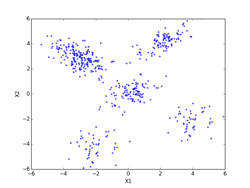
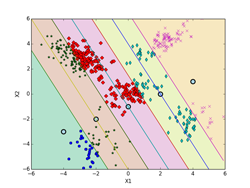
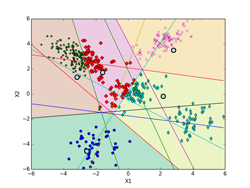
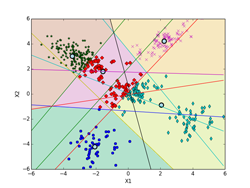
　書籍、「続：わかりやすいパターン認識」の第10章ｐ197にあるK-means法によるクラスタリングの実験を、実際にpythonで実装して確かめてみました。K-meansのアルゴリズムは、ｐ194～195（式（10.3）と式（10.19））を用いています。データは、前のEMアルゴリズムに使ったものと同じものを使っています。iter = 0の初期値は、書籍のものに合わせています。K-meansはEMアルゴリズムでσ^2 → 0の極限になっていて、実装自体はEMアルゴリズムに比べれば全然簡単です。

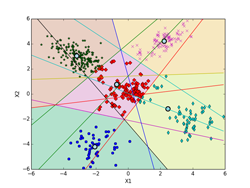
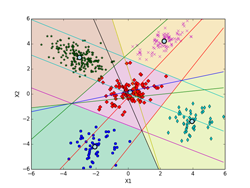
　しいて言えば、K-means法による決定境界（ボロノイ図）を描くのがちょっと面倒くさいくらいです。下記の図では、ボロノイ図は各クラスタの領域を色分けして示しています。これらの境界線は、５個の各クラスタのプロトタイプP（重心）の中から任意の２個を選んで引いた垂直二等分線（5C2で10本になります。）のどこかになります。10本の中で何本か使わない線もあります。５個のプロトタイプPの位置の関係で、どの直線のどの部分を使うかや使う本数が決まってきます。

　下記の図では、各クラスタ（ボロノイ図）に含まれる点も識別できるように色分けした違った形のマーカーで示してあります。最終的（iter=9）には、P[5][2] = [[-2.063, -4.202], [-3.018, 2.930], [0.118, 0.175], [3.942, -2.184], [2.228, 4.221]]（推定値は、 [[-2, -4], [-3, 3], [0, 0], [4, -2], [2, 4]]）に、π[5] = [0.100, 0.386, 0.218, 0.100, 0.196]（推定値は、 [0.1, 0.4, 0.2, 0.1, 0.2]）となった。

　また、K-meansは一般的には、局所的最適解になります。下記の例では、大域的最適解になっていますが、初期値の取り方や、パターンのばらつきなどによっては、局所的最適解に収束してしまいます。図で、収束状況を確認するなり、量子化誤差でエラー量が本当に最小になっているかどうかなど確認する必要があります。

　K-meansは直感的にも非常に分かりやすいので、「鶏が先か、卵が先か？」といったような哲学的な「概念の循環参照」に対する機械学習のひとつの答えにもなっています。局所的最適解に収束してしまったものの多くは死滅してしまったかもしれませんが、たまたま大域的最適解に落ち着いたものがその後繫栄した可能性は十分にあります。

  

　　　　　　　　 iter = 0                                              iter = 1

   

                         iter = 2                                             iter = 3

   

                         iter = 5                                              iter = 9

 

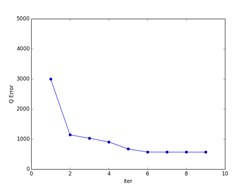
                       量子化誤差

by  チイ