K-means法によるクラスタリングの実験

　書籍、「続：わかりやすいパターン認識」の第10章ｐ197にあるK-means法によるクラスタリングの実験を、実際にpythonで実装して確かめてみました。K-meansのアルゴリズムは、ｐ194～195（式（10.3）と式（10.19））を用いています。データは、前のEMアルゴリズムに使ったものと同じものを使っています。iter = 0の初期値は、書籍のものに合わせています。K-meansはEMアルゴリズムでσ^2 → 0の極限になっていて、実装自体はEMアルゴリズムに比べれば全然簡単です。

　しいて言えば、K-means法による決定境界（ボロノイ図）を描くのがちょっと面倒くさいくらいです。下記の図では、ボロノイ図は各クラスタの領域を色分けして示しています。これらの境界線は、５個の各クラスタのプロトタイプP（重心）の中から任意の２個を選んで引いた垂直二等分線（5C2で10本になります。）のどこかになります。10本の中で何本か使わない線もあります。５個のプロトタイプPの位置の関係で、どの直線のどの部分を使うかや使う本数が決まってきます。

　下記の図では、各クラスタ（ボロノイ図）に含まれる点も識別できるように色分けした違った形のマーカーで示してあります。最終的（iter=9）には、P[5][2] = [[-2.063, -4.202], [-3.018, 2.930], [0.118, 0.175], [3.942, -2.184], [2.228, 4.221]]（推定値は、 [[-2, -4], [-3, 3], [0, 0], [4, -2], [2, 4]]）に、π[5] = [0.100, 0.386, 0.218, 0.100, 0.196]（推定値は、 [0.1, 0.4, 0.2, 0.1, 0.2]）となった。

　また、K-meansは一般的には、局所的最適解になります。下記の例では、大域的最適解になっていますが、初期値の取り方や、パターンのばらつきなどによっては、局所的最適解に収束してしまいます。図で、収束状況を確認するなり、量子化誤差でエラー量が本当に最小になっているかどうかなど確認する必要があります。

　K-meansは直感的にも非常に分かりやすいので、「鶏が先か、卵が先か？」といったような哲学的な「概念の循環参照」に対する機械学習のひとつの答えにもなっています。局所的最適解に収束してしまったものの多くは死滅してしまったかもしれませんが、たまたま大域的最適解に落ち着いたものがその後繫栄した可能性は十分にあります。

  

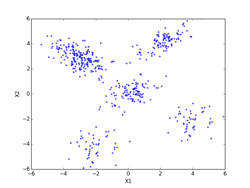
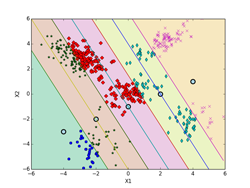
　　　　　　　　 iter = 0                                              iter = 1

   

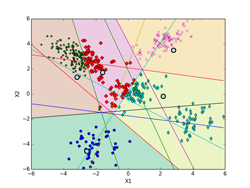
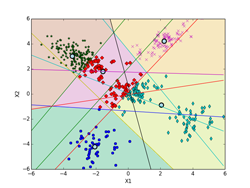
                         iter = 2                                             iter = 3

   

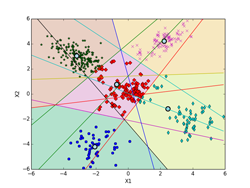
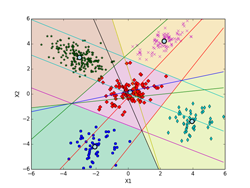
                         iter = 5                                              iter = 9

 

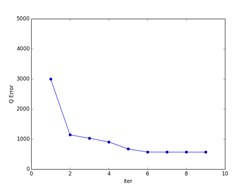
                       量子化誤差

by  チイ