モンティ・ホール問題 [学問]
最近、一般向けに書かれた人口知能の解説書の中に、「モンティ・ホール問題」という名前をよく見かけるようになりました。モンティ・ホール問題は、別名「三つの扉問題」や「三囚人問題」と同種の問題です。一見すると直観に反するような問題なのですが、最近は日本の国会でも統計で嘘をつく様な問題が取り沙汰されているので、頭の体操だと思って考えてみると面白いです。三つの扉問題とは以下のような問題です。
(問題1)
三つの扉A、B、Cがあり、司会者とゲストがいる。司会者はゲストの見ていない所で、一つの扉の後ろに賞品を隠す。ゲストに扉を選ばせ、賞品の隠されている扉(当たり)を言い当てたらゲストはその賞品を獲得できるものとする。ゲストは扉Aを選んだとする。選んだ扉を開ける前に司会者は、「私は当たりの扉を知っていますので、残った二つの扉B、Cのうち外れの扉を開けてお見せしましょう」といって実際に外れの扉を開け、確かに外れであることを確認させる。その扉がBであったとする。そして、さらに司会者はゲストに、「最初に選んだ扉Aのままでも良いですが、まだ開けていない扉Cに変えても構いません」と言う。この時、以下の問いに答えよ。
(1)ゲストが扉Aを選んだ時点で、その扉が当たりである確率を求めよ。
(2)司会者が扉Bを開けて、それが外れであることを示した時点で扉Aが当たりである確率を求めよ。
(3)ゲストのとるべき行動について、以下のいずれが正しいか?
1) 選択を変えてはならない
2) 選択をAからCに変えるべきである
3) 選択を変えても変えなくても同じである
答えは先に言ってしまうと、
(1) 1/3
(2) 1/3
(3) 2)
となります。
(問題1の解説)
S(原因)は、扉A、B、Cが当たりであることをS=ωA、S=ωB、S=ωCとすると、事前確率は
P(ωA) = P(ωB) = P(ωC) = 1/3
になります。
X(結果)は、司会者が扉Bを開けることをX=oB、扉Cを開けることをX=oCで表すことにすると、
求めたいのは、司会者が扉Bを開けたという条件の下で、扉Aが当たりである事後確率は、P(ωA | oB)であるので、
次のように場合分けをして、
(1)扉Aが当たりの場合、P(oB | ωA) = 1/2(P(oC | ωA) = 1/2)
(2)扉Bが当たりの場合 P(oB | ωB) = 0(P(oC | ωB) = 1)
(3)扉Cが当たりの場合 P(oB | ωC) = 1(P(oC | ωC) = 0)
となります。
これを条件付き確率の問題として考えると、下図1のような図が描けて、司会者が扉Bを開けて見せるのは水色部(a)、(b)となり、その内扉Aが当たりであるのは(a)の部分であるので、
P(ωA | oB) = (a) / {(a) + (b)} = 1/3
となります。
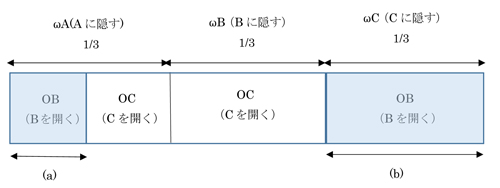
図1 司会者が正解を知っている場合
このことは、ベイズの定理を使うと、代数的にももっと明白に理解することができますが、やっていることは上の条件付き確率と同じことになります。
P(ωA | oB)
= P(ωA )P(oB | ωA) / {P(ωA )P(oB | ωA) + P(ωB)P(oB | ωB)+ P(ωC )P(oB | ωC)}
= (1/3)x(1/2) / {(1/3)x(1/2) + (1/3)x0 + (1/3)x1}
= 1/3
同様に、
P(ωB | oB) = 0
P(ωC| oB) = 2/3
となります。
(問題2)
もう一つの問題は、(問題1)の設定で、ゲストも司会者も正解を知らない場合です。すなわち、司会者、ゲスト以外の第三者が賞品を隠し、ゲストが扉Aを選んだ後、正解を知らない司会者が扉Bを開けたら外れだったという場合である。
この場合、答えは、
(1) 1/3
(2) 1/2
(3) 3)
となります。
(問題2の解説)
X(結果)は、司会者が扉Bを開けて外れであることをX=oB、当たりであることをX=oB*、扉Cを開けて外れであることをX=oC、当たりであることをX=oC*で表すと、
求めたいのは、司会者が扉Bを開て外れであることが分かったという条件の下で、扉Aが当たりである事後確率は、P(ωA | oB)であるので、
次のように場合分けをして、
(1)扉Aが当たりの場合、P(oB | ωA) = 1/2(P(oC | ωA) = 1/2、P(oB* | ωA) = P(oC* | ωA) = 0)
(2)扉Bが当たりの場合 P(oB | ωB) = 0(P(oB* | ωB) = P(oC | ωB) = 1/2、P(oC* | ωB) = 0)
(3)扉Cが当たりの場合 P(oB | ωC) = 1/2(P(oC*| ωC) = 1/2、P(oB* | ωC) = P(oC | ωC) = 0)
これを条件付き確率の問題として考えると、下図2のような図が描けて、司会者が扉Bを開けて外れであるのは水色部(c)、(d)となり、その内扉Aが当たりであるのは(c)の部分であるので、
P(ωA | oB) = (c) / {(c) + (d)} = 1/2
となります。
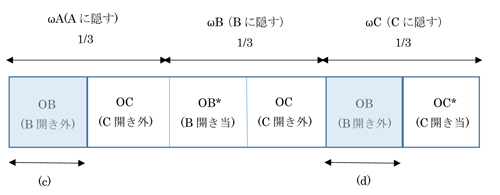
図2 司会者が正解を知らない場合
これはまた、ベイズの定理から、
P(ωA | oB)
= (1/3)x(1/2) / {(1/3)x(1/2) + (1/3)x0 + (1/3)x(1/2)}
= 1/2
となります。
同様に、
P(ωB | oB) = 0
P(ωC| oB) = 1/2
となります。
また、これらの発展形として、扉の数を3からn(>3)に増やした同様のケースも考えてみるといいかもしれません。理系の難関大を受験される方は、モンティ・ホール問題は常識として知っておいた方がいいと思います。実際にそれは条件付き確率の問題として解くことができますが、ベイズの定理を知っていれば、その理解がより深いものになると思います。ベイズの定理自体は、条件付き確率から簡単に導き出せるものなので、罹患率の簡単なベイズ更新の計算くらいはやっておいた方がいいかもしれません。
後、どうしても納得できなという人は、実際に自分でプログラムを書いて実験してみるという方法もあります。ただ、そんな時間は無いよという人のために、下記に実際にそのプログラムを公開してくれている人のURLを貼っておきました。数分くらいで、ソースコードをコピペして動かすことができます。
by チイ




コメント 0